Remarkable curl-like spirals

Alexander Gofen (2025)

Here is a family of curves specified parametrically as these integrals

or defined as ODEs:

x' = cos(sin t – kt^αcos t)

y' = sin(sin t – kt^αcos t)

All curves of this family have a property (x')² + (y')² = 1  meaning that the bullet graphing them moves with a constant speed.

Initially, I learned about these parametric curves only for k = 1 and α = 1. The graph below amazed me because it looked like curls

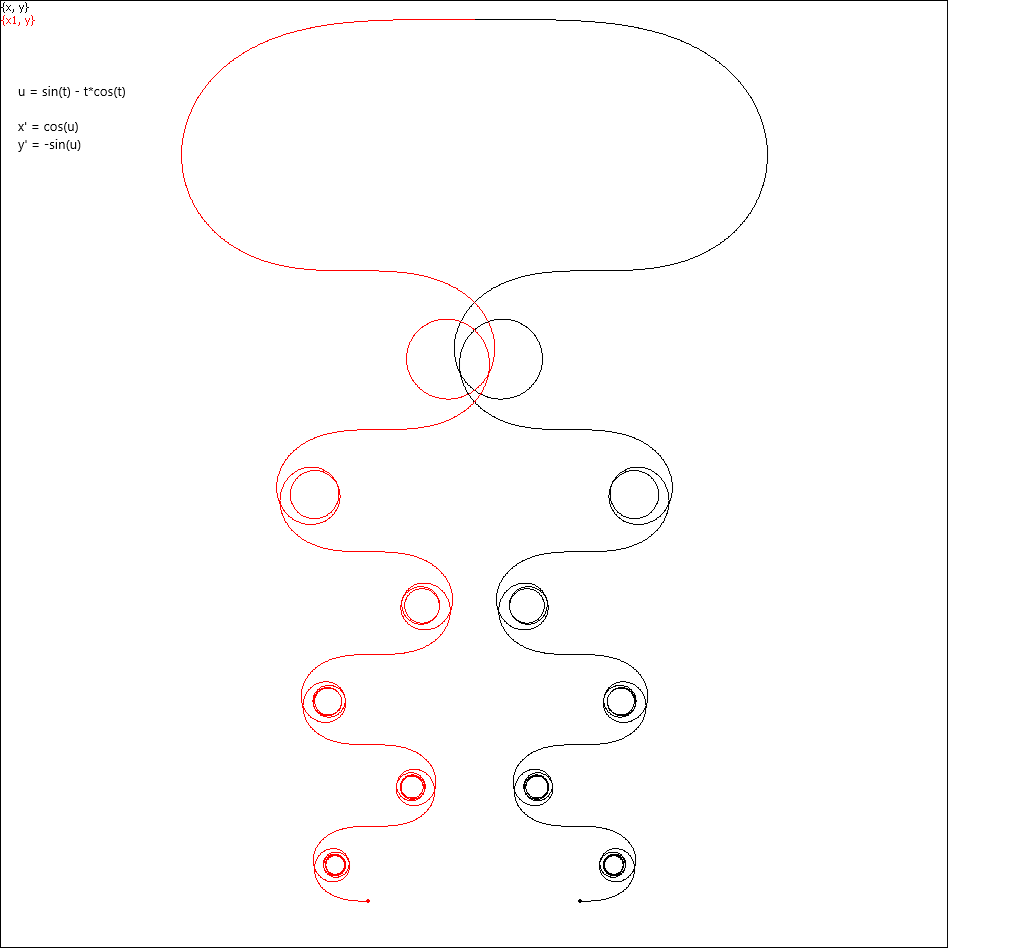
Then, just for having nothing else to do, I played a bit with the parameters. Wow! Beside looking as fancy ornaments, these curves behave like a kind of fractals, and these two parameters affect their appearance in a quite unpredictable way.

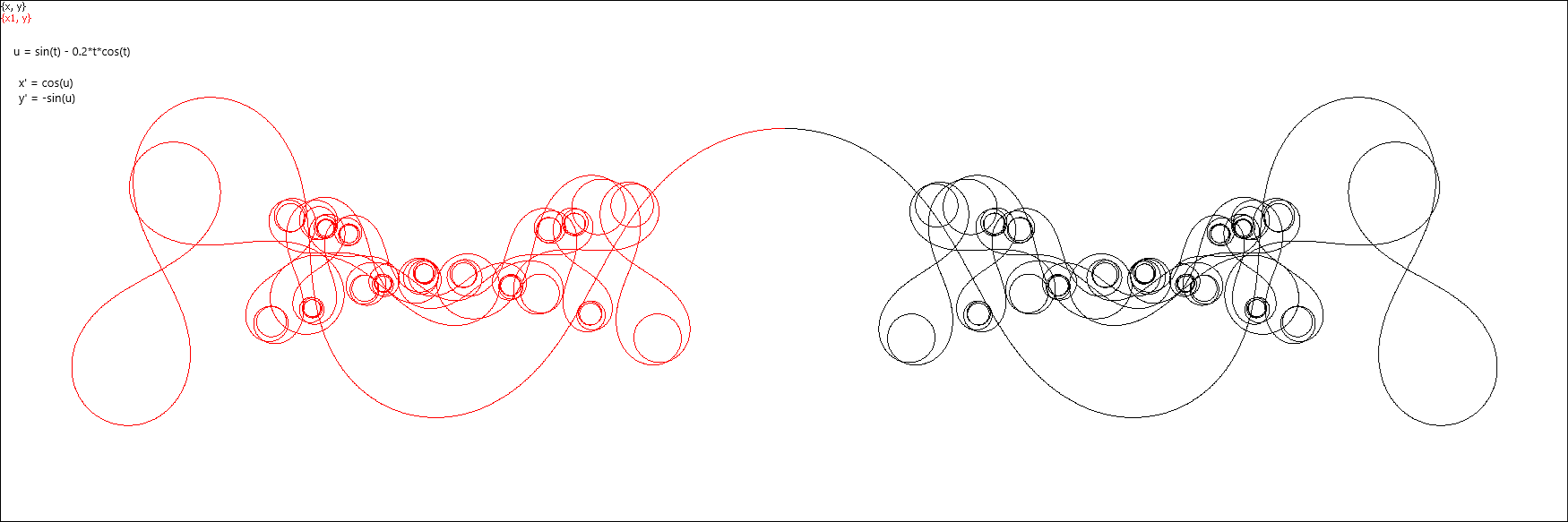
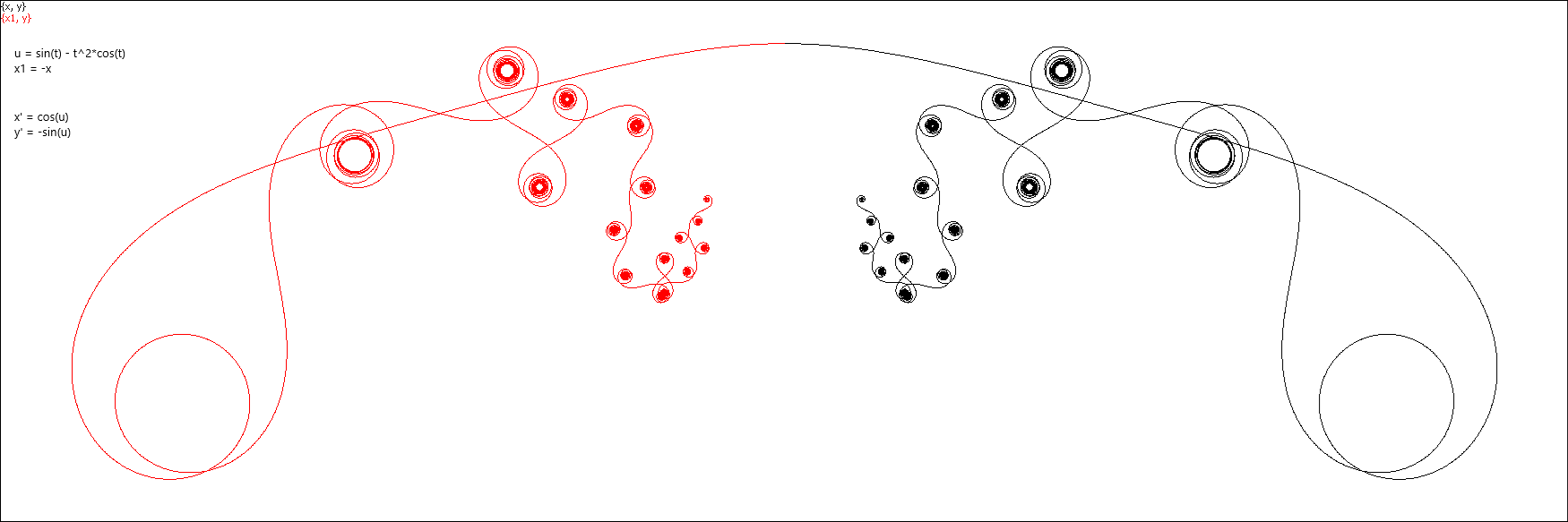
If you play this setting via TCenter, you will see a running and bouncing back "8" shape.

In order to play this and other curves in real time, download and unzip these script files.