Did the Creator of Mathematics (if He existed) leave His "Artist's signature"?

Notes on chapter 24 of the novel "Contact" by Carl Sagan, 1985.

These notes of a philosophical nature are written as a reaction to the aforementioned final chapter of the novel "Contact", where the author came up with a not quite reasonable idea of the "artist's signature".

This author's idea in itself wouldn't be worth discussing if not a possibility to suggest a better example of this kind. After the publication of the novel, something has been discovered in mathematics that could serve as an incomparably more suitable realization of the author's idea, expressed by the main character of the novel – Ellie (Eleanor).

What was the idea of the author?

Carl Sagan, just like his protagonist Ellie, worked and was an enthusiast of the SETI project (Search for Extraterrestrial Intelligence). The essence of the project was in the constant listening to space on a special radio frequency, on which the natural "noise" of space is close to zero, in the hope that some distant civilization (inside or even outside our Galaxy) would send by radio (!) some information to establish Contact. Leaving aside the (un)reality of hopes for this, in the novel such signals were detected and understood. It was a very long series of messages: one-way messages (since there can be no timely "exchange" of messages over a distance of thousands or even millions of light years).

According to the novel, these one-way messages eventually transmitted to earth a very detailed technical project for the construction of a certain machine, the principles of which were entirely unclear. The stated goal of the project was to implement a "travel" of a human from Earth to meet the Designers. And this "traveler" was Ellie… Well, it was rather, her non-physical soul, for the author was careful enough to not grossly violate the laws of physics.

When her soul has returned to earth after communicating with such a super Mind and realizing Its unimaginable power, Ellie wondered: could it be that such a Mind was capable of creating mathematics according to Its own project? To create it – and leave its "signature", as artists do on canvases?

Ellie concluded that this "signature" should be sought in the infinite fraction of some important irrational number in mathematics, say π. The book ends with the moment when the computer program discovers in the binary infinite fraction of π such a segment that is easily interpretable as a bitmap file of a circle! This coarse image of a circle, found in the binary expansion of π, impressed Ellie so much that she acknowledged it as the "signature of the Artist" who "created mathematics". However, such a rough outline of a circle encoded in π would be hardly an impressive "signature" appropriate to the hypothetical Creator of mathematics. Below we will consider ideas of such signatures much more impressive for such a goal!

Let's examine the idea of the "signature" in more detail.

"Artist's signature?"

Let us note right away that the metaphor of "artist's signature" is not acceptable in this context at all. "Signature" is something arbitrary. An artist may or may not put it; to sign his name in printed letters, or in script, or only initials. The irrational number π is defined in mathematics as the only solution of certain equations, or as the (existing, and therefore unique) limit of certain sequences. There cannot be mathematics in which the length of a circle with unit diameter in Euclidean geometry[1] differs from the already known value of π. So, there is no freedom of "signature" in the number π (or in some other irrational numbers "popular" in mathematics).

Then, is it possible to "save" Ellie's expectations of discovering in mathematics "a certain sign" from its creator? Is it possible to discover in mathematics a certain surprise, completely shocking for a human researcher of mathematics (but always known to its true "Creator")?

The following text will demonstrate the existence of such a shocking surprise, but we will have to switch from the metaphor of the "artist's signature" to another metaphor, namely...

Paintings admitting several interpretations.

There have been many such paintings in the history of art! Their various (completely unrelated!) interpretations are conceived by the artists themselves, while some mental effort may be required from the viewer to "switch" from one interpretation to another.

In relation to mathematics, this metaphor has the meaning of an attempt to discover some not yet noticed "picture" in a known object, maybe even in the number π. In other words, we are talking about searching for some as yet unknown secondary property or a double-purpose feature in an already known mathematical object, where the secondary purpose of the object follows from the primary one, or is a statement equivalent to the primary one, or it is appearance of the known object in a previously unknown context. There exist already many such situations in mathematics. Here are a couple of simple examples.

Let the primary property be the set of numbers divisible by 3. We can easily define the general form of such numbers n, where n = 3k (for any natural k). However, another property of the set of numbers divisible by 3 is known from elementary arithmetic (though it takes place only in the decimal system): the sum of the digits of numbers divisible by 3 is also divisible by 3 – and this is a secondary property that Ellie could have "discovered" with surprise (if she had not "gotten used" to it in elementary school).

The number π itself was first defined by the ancient Greeks in geometry as the limit of a certain convergent sequence expressing the circumference of a circle of diameter 1. However, centuries later, mathematicians discovered that the number π also appears in contexts unrelated to geometry: for example, as the value of the Gamma function Г(1/2) = √π . Gamma function is the extension of the integer-valued function factorial n! to real and complex numbers. What does the circumference have to do with the factorial?!

The number π appears also in some expressions containing the Euler's Zeta-function

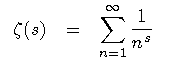
– a centerpiece of the number theory. For example, for an even arguments 2k

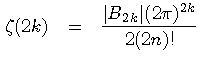
(where B_2k are the Bernoulli numbers). Here is another formula for the ζ containing π

and number π appears in sophisticated formulas discovered by Ramanujan. How can a circumference, factorial, and number theory have any interrelation between each other?!

It's so appropriate here to recall the opening conversation in the remarkable article by [Wigner].

A statistician showed a reprint to his classmate. The reprint started, as usual, with the Gaussian distribution. Then the statistician explained to his classmate the meaning of the symbols for the actual population, for the average population, and so on. His classmate was a bit incredulous and was not quite sure whether the statistician was pulling his leg.

“How can you know that?” was his query. And what is this symbol here?”

“Oh,” said the statistician, “this is π.”

“What is that?”

“The ratio of the circumference of the circle to its diameter.”

“Well, now you are pushing your joke too far,” said the classmate, “surely the population has nothing to do with the circumference of the circle.”

It all is an illustration of the phenomenon of the presence in mathematics of mysterious "reusable" objects of secondary and tertiary purpose. Therefore, we will further look for the "secret sign" of the Creator among such secondary properties.

But first, let's finish with the question…

What can be "encoded" in irrational numbers.

Irrational numbers were discovered by the ancient Greeks as numbers that cannot be represented as a fraction m/n with integer m and n. The Greeks proved that, for example, √2 is irrational. In later times, an equivalent definition of irrational numbers arose as infinite decimal (or in another number system) fractions that have no period (cannot be represented as repeating segments of digits).

There are two opposite approaches to obtaining irrational numbers:

1. Constructing some irrational number using a given algorithm unrelated to the solution of any problem.

2. Solving some problem, the solution of which turns out to be an irrational number.

For example, in case (1), using an obvious simple algorithm, one can construct an irrational number a whose infinite fraction is the sequence s = {101001000100001.... }. We do not know if the number а is a solution of some meaningful problem, or if it possesses any special property but being merely the output of this algorithm.

Moreover, with such an approach, it is easy to compose an irrational number, the digits of which encode any desired message, even the entire Bible; or encode any image. And after those digits, to add the digits of the sequence s, which altogether will also make some irrational number.

It is clear that approach (1), suitable for encoding everything, is not what Ellie was interested in. She was interested in approach (2), because π and some other "popular" irrational numbers in mathematics arise as solutions to special problems.

For example, an algebraic irrational number √2 is a solution of the equation x² = 2, е – a solution of non-algebraic equation ln x = 1, the number ln 2 is a solution of e^x = 2, and π – one of the solutions of sin x = 0.

As already said, π and other irrational numbers mentioned above are the only solutions to the corresponding equations. Therefore, even the omnipotent Creator of the universe does not have the freedom to change anything in the only solution to a mathematical problem. Thus, we are trying to understand whether the sequence of digits of irrational solutions to some known problems can contain a certain informative segment (a special sign of the Creator) as a secondary property of those solutions.

We have already seen in the example of the sequence s that the corresponding irrational number contains segments of only one specific type (rather than any), and only with the digits 0 and 1.

On the other hand, there is the concept of the normal irrational number (by analogy with the normal distribution in probability theory). By definition, in a normal irrational number with base b, every segment of digits of length n appears with the same probability b⁻ⁿ (where b is the base of the numeric system). Such numbers exist and have been constructed. According to the Borel's theorem, in a normal number any desired sequence will occur with probability 1. For a normal irrational number, therefore, Ellie's wish is trivially satisfied for any desired image or sequence of digits.

The problem is, however, that none of the popular irrational numbers such as √2, π, or e have been proven to be normal irrational numbers (2024), although computer experiments suggest they may be. If so, then π contains somewhere in its expansion any image or any desired message, as well as its negation, and its versions with grammatical errors... Not to mention that "somewhere" in an infinite sequence means anywhere far. Yet it will never be possible to search further than, say, 10⁵⁰ decimal digits on any computer.

Thus, Ellie's very idea of finding in π some special graphic image – a sign from the Creator of mathematics – made no sense.

Then, where else in mathematics does it make sense to look for any objects of secondary purpose as a graphic image?

Ulam spiral

The primes and the laws of their distribution are the oldest topic in mathematics with still unsolved problems. If we mark the positions of prime numbers on a straight line, we will see that they appear less and less often, but are distributed irregularly, and in some sense "randomly". Here is why. Though the primes are distributed less and less frequently (in accordance with the already known asymptotic estimates), the so-called twin primes[2], i.e. pairs that differ by only 2 (or pairs that differ by 4), occur wherever far away from the beginning. It is namely such pairs of close primes among the increasingly rare remaining primes that create the impression of randomness in their distribution on a straight line.

However, if we plot the natural numbers not on a straight line, but on a plane in a certain regular way, then a surprise awaits us, called the Ulam spiral (or carpet) [Ulam].

Ulam spiral (courtesy to - Wikipedia).

A regular plot of natural numbers on a plane can be made either along the Archimedean spiral or along the "square spiral". The surprise is that the points of prime numbers on this Ulam spiral (plotted in brown on the picture above) are distributed approximately evenly (unlike on a straight line). At that, some segments of straight lines will be clearly noticeable in this carpet!

This phenomenon of concentration of primes on straight lines within the Ulam spiral follows from another phenomenon discovered by Euler. It turns out that some square trinomials generate prime numbers in quantities higher than other polynomials. Such is, for example, the Euler's square trinomial n² – n + 41 yielding primes for n = 1, ..., 40.

When natural numbers are plotted on a plane along one of the above-mentioned spirals, the points located on the diagonals belong to various square polynomials, so that those of them that generate abundant primes create the effect of straight-line segments saturated with primes.

There are no segments densely filled with primes in Ulam's carpet, but the very fact of their concentration on straight line segments is surprising and could well be a suitable candidate for the "special sign" searched by Ellie: suitable batter than the coarse image of a circle encoded in the digits of π.

But the most suitable and surprising candidate for a special sign is...

Fractals and the Mandelbrot set.

Now I will try to demonstrate that the graphical image of the Mandelbrot set is the most striking special sign that Ellie and Sagan could have ever dreamed of!

If you look at the picture of the Mandelbrot set from afar

Fig. 1. The Mandelbrot set (courtesy to Wikipedia).

at first glance it may seem hardly different from pictures of other well-known sets whose boundaries are defined by some algebraic equations (below).

For example, the unit circle is defined by the equation х² + у² = 1, and the corresponding disk – with the inequality х² + у² < 1. Or…

The equation у = ± (1 – х²)^1/2 + х^2/3 defines a "Heart".

The boundaries of sets defined by algebraic equations are "simple" piecewise-smooth curves. Let us note this fact.

The Mandelbrot set M is also defined using the simplest algebraic equation on the complex plane, with the only difference being that the criterion for belonging to the set is not the fulfillment of an inequality, but by the fact of the boundedness or unboundedness of some iterative sequence based on a given algebraic equation.

Specifically, a point c in question on a complex plane belongs to M if the iterative sequence {z_n}

z_n₊₁ = z_n² + c, z₀ = 0, n = 0, 1, 2, ....

is bounded. Otherwise, c does not belong to М.

It turns out that the boundary of the set M is not a simple piecewise-smooth curve of finite length, as in the examples above. If we take a close look at the static picture of the set (Fig. 1), we notice that its contour, approximately similar to a cardioid, contains a number of protrusions of different sizes. Zooming in further, it turns out that each of the protrusions in turn contains all sorts of "pretzels" and curls, somewhat similar to the previous ones, but not exactly. With the help of a computer, you can continue to "peer" into each of the details with ever-increasing magnification, discovering new and new curls and details: and so on ad infinitum.

The Mandelbrot set

in a process of infinite zooming in (courtesy to Wikipedia)

The boundaries of such an infinitely complex structure are called fractals.

The Mandelbrot set has a rich list of properties (see Wikipedia), in one of which appears … Guess what?

The number π! (Ellie, do you hear me?!)

And now, realizing with awe the infinite complexity and beauty of the Mandelbrot set – a purely abstract object entirely outside of this world, it is so appropriate to quote the words of Sir Roger Penrose about the phenomenon of the Mandelbrot set:

Though being purely abstract, this exotic structure is as much "out there" (in our reality) as Mount Everest is, subject of exploration in the way a jungle is explored [Penrose].

Isn't this that amazing "sign" from the Creator of Mathematics that Ellie was looking for?!

It should be noted, that the Mandelbrot set is by no means the only currently known fractal. Besides being the first of such fractals, the M set is especially convenient for study because it has a simple criterion for the boundedness of the sequence (not the case for other, more complex sets).

And finally, let's philosophize a little.

Can Mathematics Have a Creator?

It is not at all natural that "laws of nature" exist, much less that man is able to discover them. (E. Schrödinger)

The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it and hope that it will remain valid in future research and that it will extend, for better or for worse, to our pleasure, even though perhaps also to our bafflement, to wide branches of learning. (E. Wigner)

In order to discuss this topic, first it is necessary to accept one or another of the existing philosophical axiomatics concerning what all things consist of. Dualism, for example, recognizes the existence of both the Physical (material) world and that of Abstractions or ideas. The world of Abstractions or ideas is also called the Platonic universe. (I adhere to the philosophy of trialism, that there exists also the third component – the world of Consciousness and Soul).

In this system of things, mathematics, as Roger Penrose noted, is a special section of Platonic universe in the following sense. The Platonic universe (similarly to the Internet) contains all possible ideas: right or wrong, truths or lies, sequences that make sense and those that don't.

But among all this, only mathematics is the absolute truth in a sea of other arbitrary abstractions of the Platonic universe.

· Mathematics, being a system of pure abstractions, is totally outside of the physical world, so that not a single concept of mathematics is found in the physical world. However, at the same time...

· The miraculous appropriateness of mathematics for the formulation of the laws of physics does take place [Wigner], manifesting the fact, that those abstractions, nevertheless, are suitable for modelling the physical world, even if only approximately! May it be so because the Creator of the physical world designed His creation using mathematics?!

· Unlike the physical world, mathematics could not have a moment of creation. Mathematics exists independently of the physical world, and also independently of whether there is any person, or other mind, who tries to understand it. Moreover...

· Another reason why mathematics could not be "created" is because the act of creation implies that the Creator considers different "possible" versions and settles on one of them. However, mathematical truths cannot be multivariant. There cannot be a version of mathematics in which, say, the number of primes is finite. Or the solution to an equation that has a unique solution has become different. Or some object of secondary purpose has ceased to be such, say Г(1/2) ≠ √π .

· And finally: it is mathematics itself (the Gödel's theorem) proving that there exist mathematical statements that cannot be proven. Therefore, such statements will always remain open and unverifiable for humans.

The above set of characteristics can only be inherent in the Creator of the universe, Who, just as mathematics, is outside the physical world and Who has existed always. Therefore, mathematics is one of the manifestations of the Creator. Therefore, while Augustinian philosophy views mathematics as part of God's eternal truth, I view mathematics as a part of the God's own mind.

Alexander Gofen

2024

References

[Wigner] Eugene Wigner "The Unreasonable Effectiveness of Mathematics in the Natural Sciences"

https://www.hep.upenn.edu/~johnda/Papers/wignerUnreasonableEffectiveness.pdf

[Ulam] https://en.wikipedia.org/wiki/Ulam_spiral

[Mandelbrot] https://en.wikipedia.org/wiki/Mandelbrot_set

[Penrose] Roger Penrose, "The Emperor's New Mind", 1989.

[1] In the geometry on a sphere of radius r, for example, the diameter (i.e. a semi meridian) of a big circle is πr, and the length of the circumference of a big circle (i.e. of the equator) is 2πr. However, the known value π applies only for circumferences in Euclidean geometry on a plane.

[2] In the beginning, we have twin primes (3, 5), (5, 7), ..., (29, 31). The biggest pair discovered in the moment (2022) is 2996863034895 × 2^1290000 ± 1. Though the pair as big as this is found, it's not known if the set of twin primes is infinite or finite.