Special cases of triangle congruence
in free fall periodic orbits
12 cases with unit masses
and
4 cases with masses 1, 0.8, 0.8
By Alexander Gofen (February 2022)
|
This is a gallery of still images of high-resolution trajectories explained below. In order to watch real-time animation of these trajectories, it's necessary to download and run the Taylor ODE solver according to the following instructions. Visit http://taylorcenter.org/Gofen/TaylorMethod.htm looking for the downloading instructions of the zipped file http://taylorcenter.org/Gofen/TaylorCenterDemo.zip According to the instruction, extract it all and run the only executable TCenter.exe (not changing the content of the folder). After the welcome screen… 1) Go to Demo/3 bodies/Periodic (free fall)/Run a simulation #.... 2) Enter a number of the desired sample between 1 and 30 into a small window (top left). The program loads the ODEs for the 3-body problem with the initial values corresponding to the selected periodic orbit, compiles, and integrates the problem until reaching the termination point – the period of this simulation. 3) When the integration reaches the termination point (the period), the program displays the message. As you click OK, the program opens the Graph window displaying the entire trajectory. You may wish to Play it as a real time animation during certain time (by default the duration is 25 s). Depending on the complexity of the curve, it may require duration something like 60-80 seconds. Click Play button and enjoy the show. Then repeat everything from step 2 for another sample. 4) While in the menu Periodic (free fall), you may choose a couple of specific numbers (#1, #18). Then click Play button. |
Below we introduce a gallery of 12 orbits of the 30 cases of periodic "free fall" in the 3-body problem (*) having unit masses: "free fall" meaning that the initial velocities in all 3 masses are zero. All 30 cases present periodic motion with a particular periods T, and their numbering follows the table of the initial values in (*).
(*) Xiaoming Li and Shijun Liao, Movies of the Collisionless Periodic Orbits in the Free-fall Three-body Problem in Real Space or on Shape Sphere
http://numericaltank.sjtu.edu.cn/free-fall-3b/free-fall-3b-movies.htm
An extensive mathematical explanation and the history of the problem are in the
article "Dropping bodies" by Richard Montgomery
https://doi.org/10.1007/s00283-022-10252-4
https://link.springer.com/content/pdf/10.1007/s00283-022-10252-4.pdf
The
selected 12 simulations are special in that the initial triangle formation of
rest at t=0 happens to be congruent to the second triangle formation of
rest at the moment t=T/2. The moments of rest (0 and T/2) will be also referred as the break
points.
The congruent triangles are plotted in gray.
Of those 12 congruencies, there are 9 cases where the triangles in the pairs
relate via reflection, and 3 cases when the triangles in the pairs are in
central symmetry.
The table of all the 30 orbits
Here we summarize the newly
discovered properties in 12 of the 30 orbits. The Table 1 below shows in which
of the 30 simulations (*) these earlier unknown properties take place.
We consider two triangular formations of the 3 bodies: the initial △ABC at the moment t=0 and the second △A′B′C′ at the moment t=T/2, where
△ABC and △A′B′C′
are congruent: with or without reflection. This means the equality of the
corresponding angles ∠A=∠A′,
∠B=∠B′,
∠C=∠C′.
Let the bodies #1, #2, #3
at the initial moment reside correspondingly at the vertices A, B, C of the △ABC. Their trajectories, however, may not necessarily
lead to the corresponding vertices A′, B′, C′ of the △A′B′C′, as some of the simulations
below demonstrate. Among the data collected by the special research program,
there are the permutations (αβγ), where the identity permutation
is denoted Id = (123). In the case of the Id
permutation, the trajectories of the bodies #1, #2,
#3 lead from the vertices A, B, C to the
corresponding vertices A′, B′, C′ (no matter whether △A′B′C′ is a reflection of △ABC or not).
These newly discovered properties in the 12 of the 30 follow
below (the numbering begins with 3 in order to match the numbering in this article).
3. In the moments (1/4)T and (3/4)T the bodies are either in syzygy (Case 5), or they form an isosceles triangle (Case 6).
4. The triangle formation at the second moment of rest (1/2)T is congruent to the initial triangle.
5. In 3 of the 12 orbits in the moments (1/4)T and (3/4)T the second triangle is a result of 180˚ rotation of the initial triangle so that both triangles and respective parts of orbits are symmetric over the central point lying on the syzygy, one of the bodies being in the middle. At that, the three vectors of the velocities in the moments (1/4)T and (3/4)T are reciprocally parallel. However...
6. In the remaining 9 orbits the edges of the triangles in pairs are not parallel as both triangles are in the relation of reflection, i.e. the two respective parts of orbits are symmetric over some line of symmetry which, however, is not necessarily the line of syzygy. Specifically...
7. If there is no permutation (i.e. Id takes place), then in the moments T/4 and (3/4)T the 3 bodies are in syzygy on the line of symmetry, otherwise in the moments T/4 and (3/4)T the bodies are not in syzygy forming an isosceles triangle (Robert Montgomery).
|
At t = T/2 |
At t = T/4 |
|||||
|
# |
Congruency |
Parallel edges |
Symmetry |
Permutation |
Isosceles |
Syzygy |
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
4 |
Yes |
Reflection |
(321) |
Yes |
||
|
5 |
||||||
|
6 |
Yes |
Reflection |
(321) |
Yes |
||
|
7 |
||||||
|
8 |
Yes |
Reflection |
Id |
Yes |
||
|
9 |
||||||
|
10 |
Yes |
Reflection |
Id |
Yes |
||
|
11 |
||||||
|
12 |
||||||
|
13 |
||||||
|
14 |
Yes |
Yes |
Central |
(132) |
Yes |
Yes |
|
15 |
Yes |
Yes |
Central |
(132) |
Yes |
Yes |
|
16 |
||||||
|
17 |
||||||
|
18 |
Yes |
Reflection |
Id |
Yes |
||
|
19 |
Yes |
Reflection |
(213) |
Yes |
||
|
20 |
||||||
|
21 |
||||||
|
22 |
Yes |
Reflection |
Id |
Yes |
||
|
23 |
||||||
|
24 |
||||||
|
25 |
Yes |
Reflection |
Id |
Yes |
||
|
26 |
||||||
|
27 |
Yes |
Yes |
Central |
(213) |
Yes |
Yes |
|
28 |
||||||
|
29 |
Yes |
Reflection |
Id |
Yes |
||
|
30 |
||||||
How the triplets of initial points were obtained
As explained in (*), the
authors fixed the points q1 = (-0.5, 0), q2 = (0.5,
0), while the goal of the search algorithm was to obtain points q3 such
that the target function be near zero with the specified accuracy. (The target
function was defined so that it reaches zero when a period is found). Below is
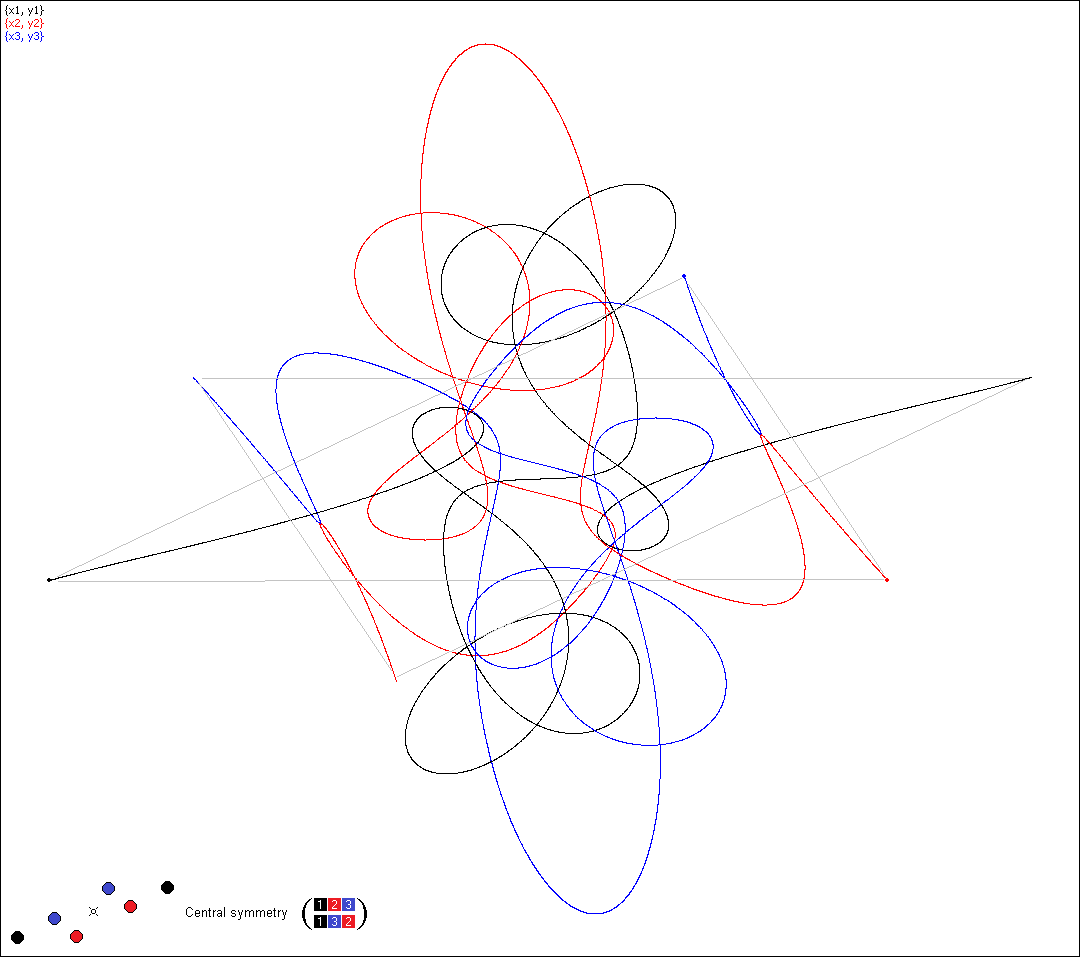
a scattered graph for the 30 points q3 obtained in the search process (*):
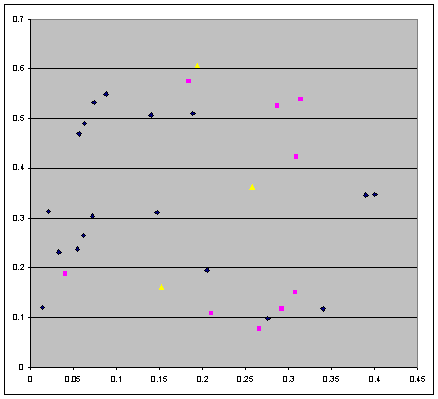
Figure 1. The 30 values for the third initial point q3 obtained in
a search algorithm
The three yellow points correspond to the cases of the central symmetry, the 9
magenta points correspond to the cases of reflection, and the remaining blue
points correspond to the orbits with no special properties. This graph does not
reveal any remarkable pattern. There is no mentioning in (*) whether the search
algorithm delivered all existing points q3 in the given bounded area
of search, and whether the number of points q3 is
finite or infinite.
9 cases of congruence with reflection
In these 9 cases of
congruence with reflection, the two triangles are in the relation of reflection
over a certain line of symmetry (in yellow), and also the entire trajectories
have the same line of symmetry. In some of the following 9 cases with
reflection, a non-Id permutation takes place, meaning that the trajectory
of a body #i (1 ≤ i ≤3) starting at a vertex X
reaches a vertex Y ≠ X, X, Y ∈
{A, B, C}. If this is the case, the geometrically respective vertices would
have different colors in accordance with the moving body color.
With a non-Id permutation, at the moments T/4 and 3T/4 the
3 bodies are not in syzygy (for example, simulation 4) making an isosceles
formation instead.
Otherwise, in the case of the Id, at the moments T/4 and 3T/4
the 3 bodies are in syzygy which is also the line of symmetry (for example,
simulation 8).
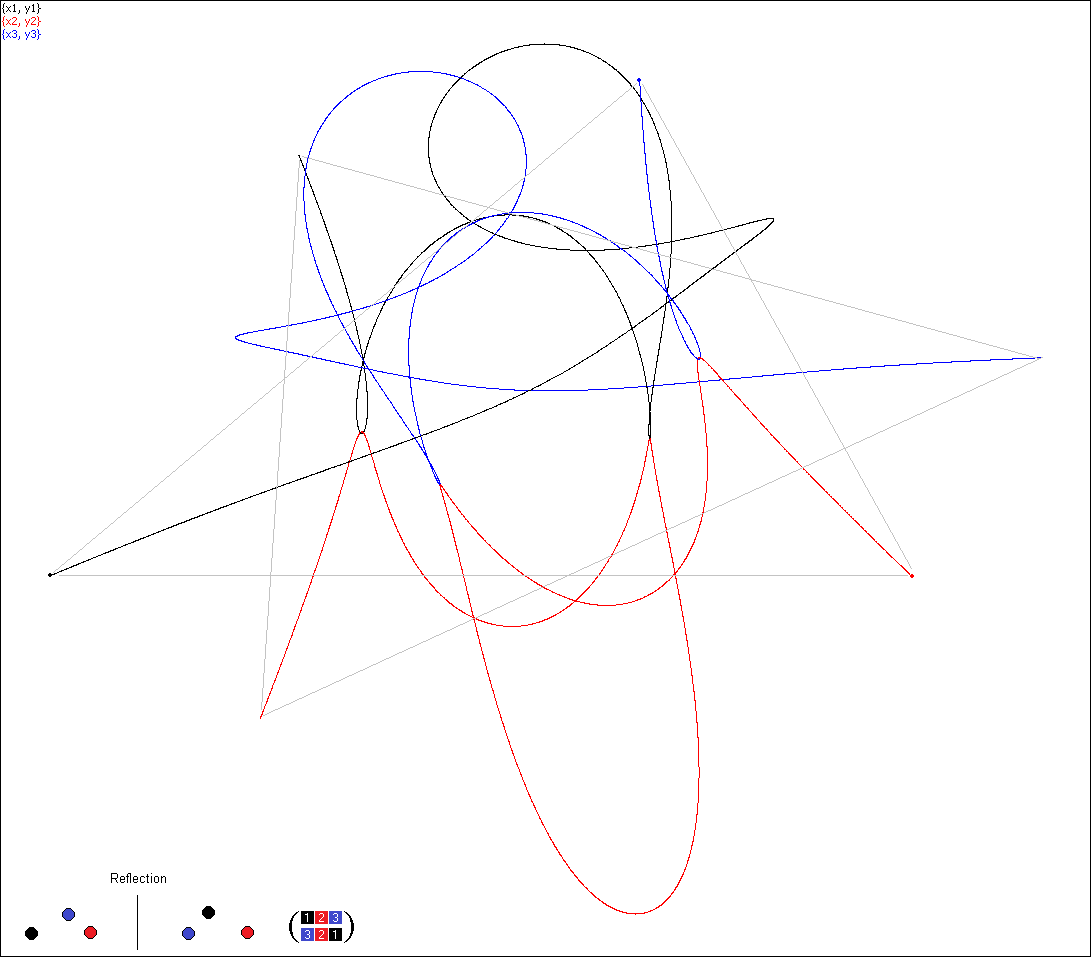
Simulation 4, permutation (321)

Simulation 4. At the moment T/4 the bodies are in an isosceles formation
(rather than in syzygy).
The yellow line is the axis of symmetry.

Simulation 6, permutation (321)

Simulation 8, no permutation (Id)

Simulation 8. At the moment T/4 the bodies are in syzygy, rather than in
an isosceles formation.
The line of syzygy (in gray) is also the axis of symmetry.

Simulation 10, no permutation (Id)
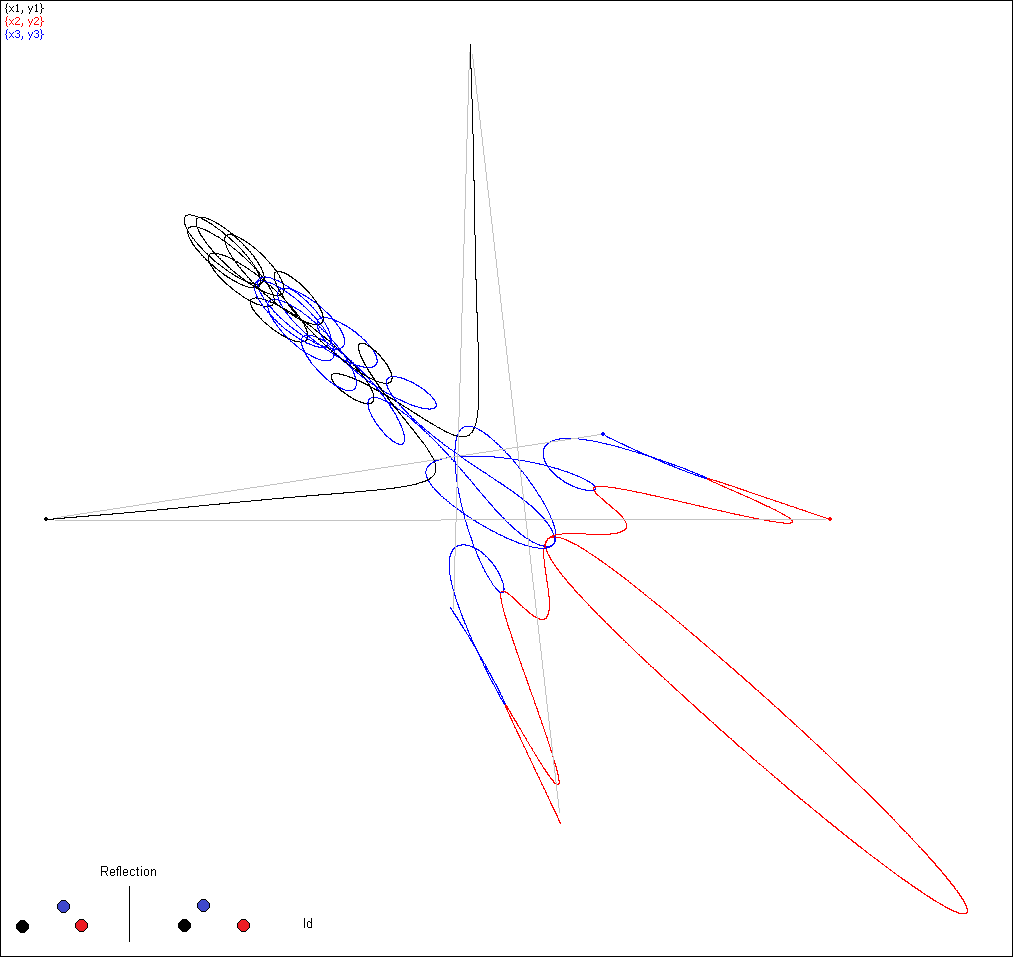
Simulation 18, no permutation (Id)
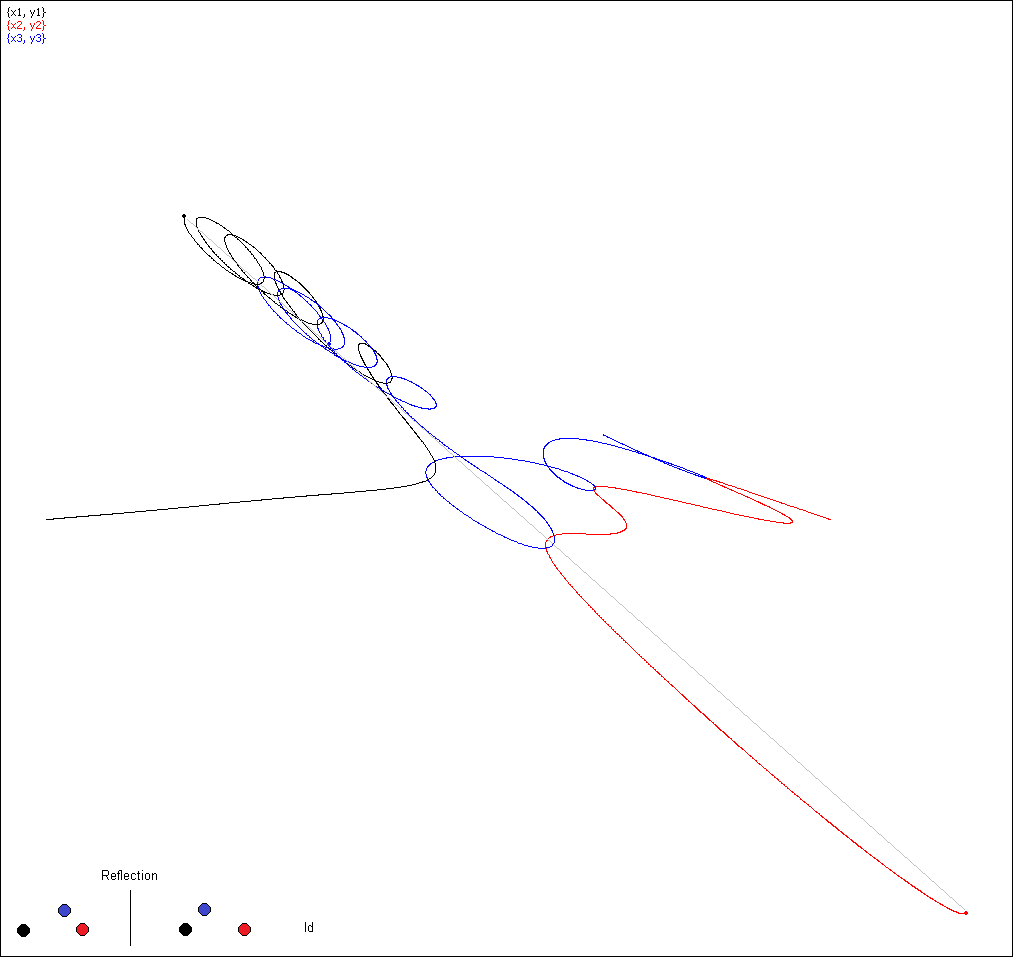
Simulation 18: no permutation so that the bodies are in syzygy at T/4 which is
also a line of symmetry
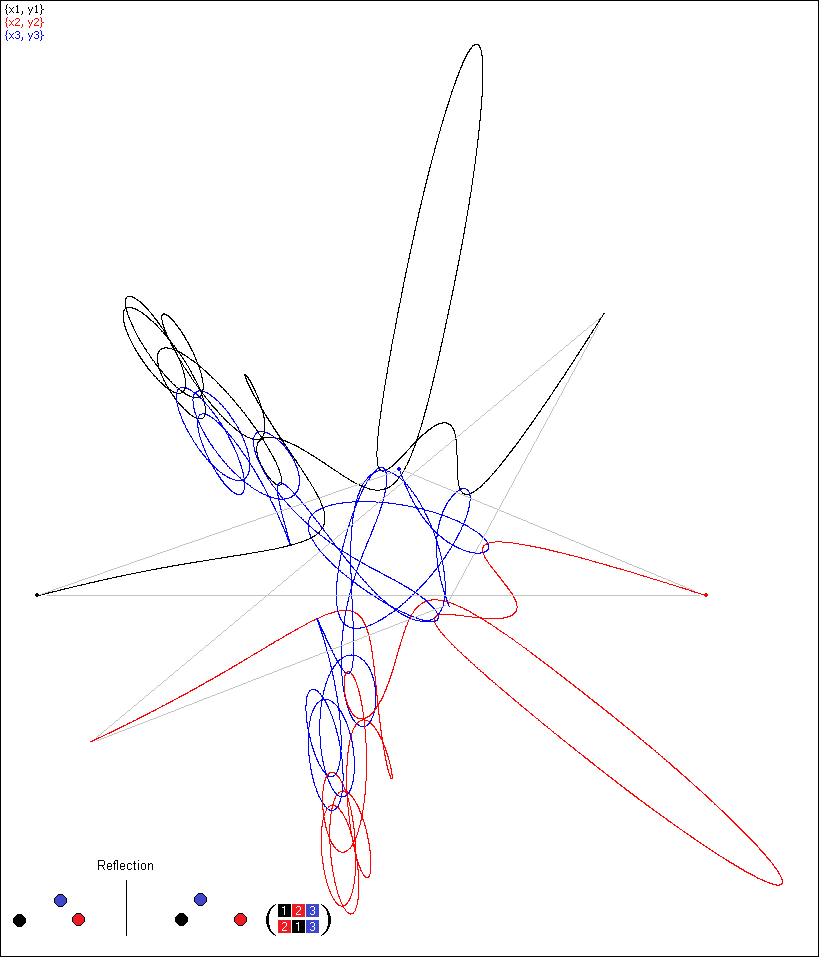
Simulation 19, permutation (213)

Simulation 19, permutation (213)
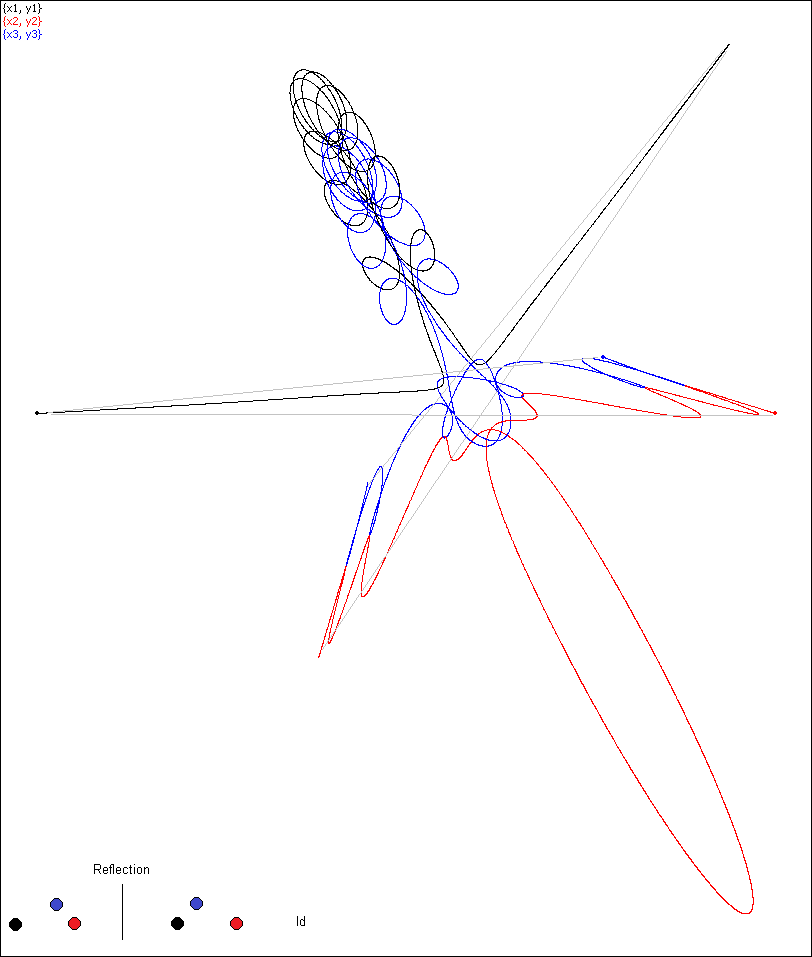
Simulation 22, no permutation (Id)
Simulation 22, no permutation (Id). The bodies are in syzygy at
T/4

Simulation 25, no permutation (Id).

Simulation 25, no permutation (Id). The bodies are in syzygy at T/4

Simulation 29, no permutation (Id)

Simulation 29, no permutation (Id). The bodies are in syzygy at T/4
3 cases of congruence
with central symmetry, 180˚rotation,
and non-Id permutation
so that at t=T/4 a syzygy
takes place, one of the bodies being in the middle.

Simulation 14, permutation (132)

Simulation 14 at the moment T/4
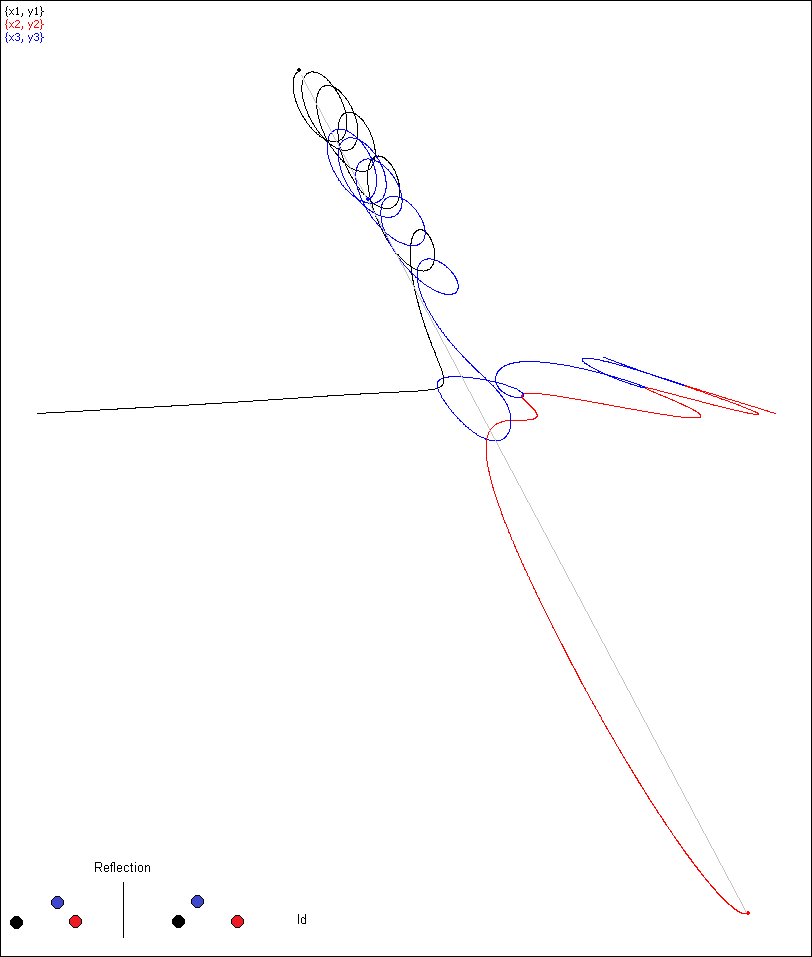
Simulation 15, permutation (132)
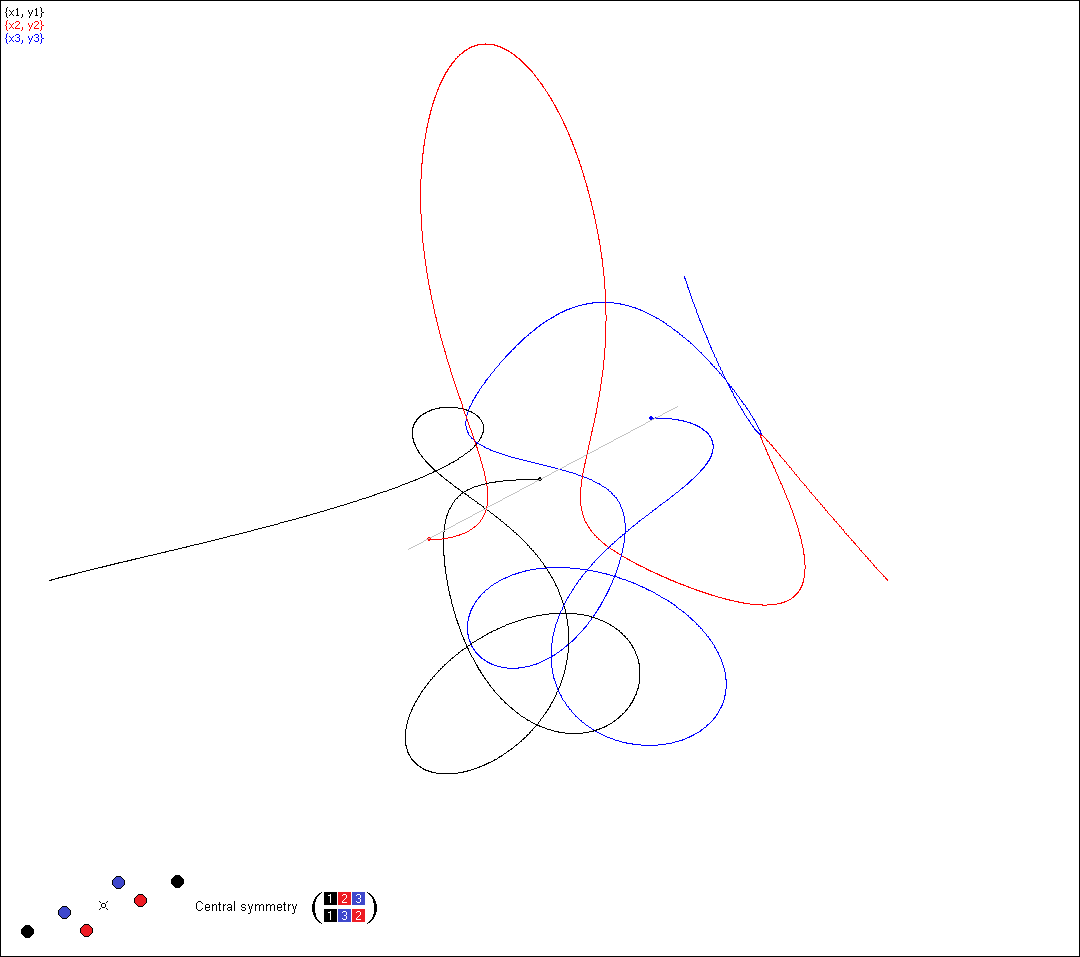
Simulation 15 at the moment T/4

Simulation 27, permutation (213)

Simulation 27 at the moment T/4
4 cases with
masses 1, 0.8, 0.8
|
At t = T/2 |
At t = T/4 |
|||||
|
# |
Congruency |
Parallel edges |
Symmetry |
Permutation |
Isosceles |
Syzygy |
|
1 |
Yes |
Reflection |
Id |
Yes |
||
|
2 |
||||||
|
... |
||||||
|
23 |
||||||
|
24 |
Reflection |
Id |
Yes |
|||
|
25 |
||||||
|
26 |
Yes |
Reflection |
(132) |
Yes |
||
|
27 |
Yes |
Reflection |
Id |
Yes |
||
|
28 |
||||||
|
29 |
||||||
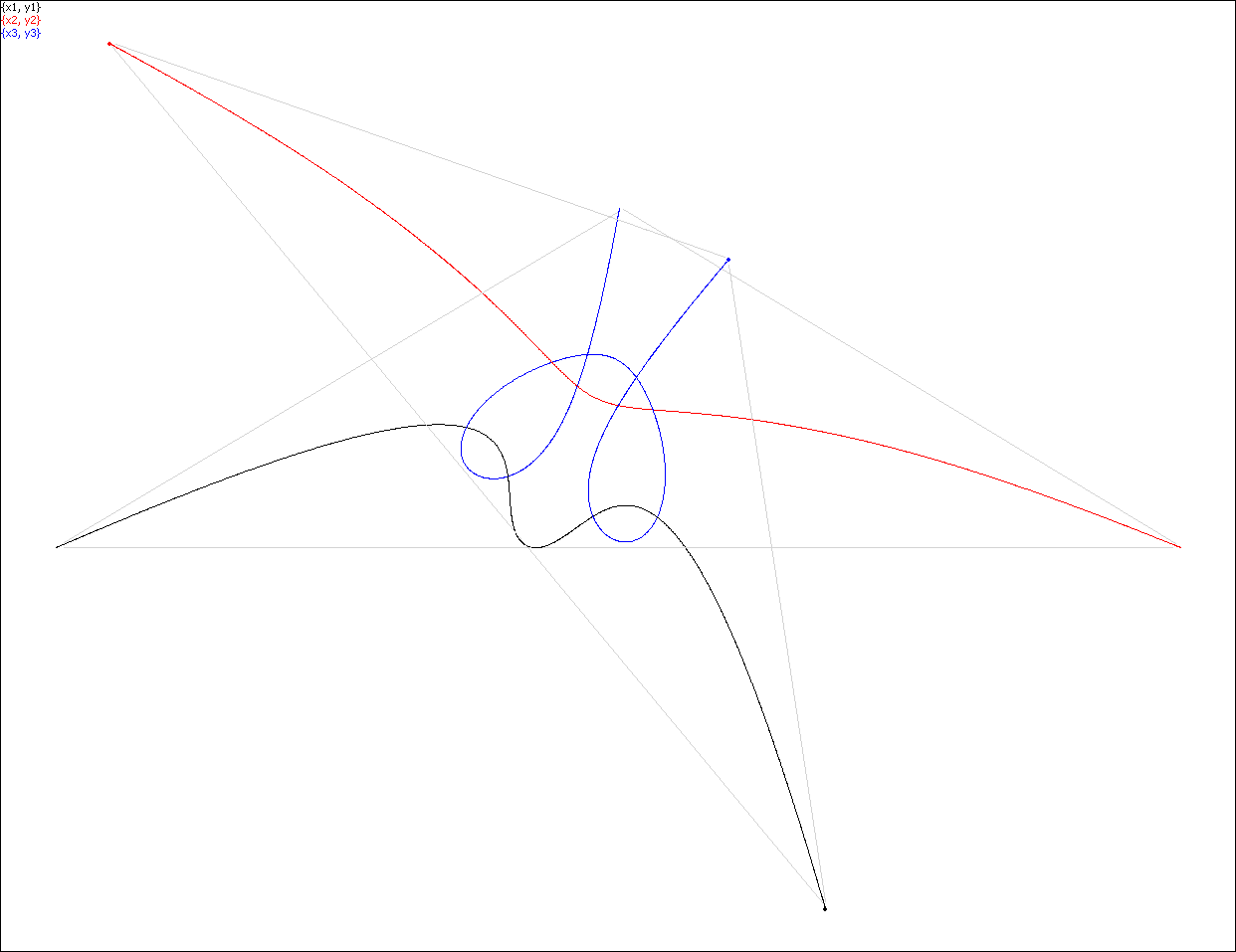
Simulation 1. No
permutation.

Simulation 1. At the moment T/4 the bodies are in syzygy.
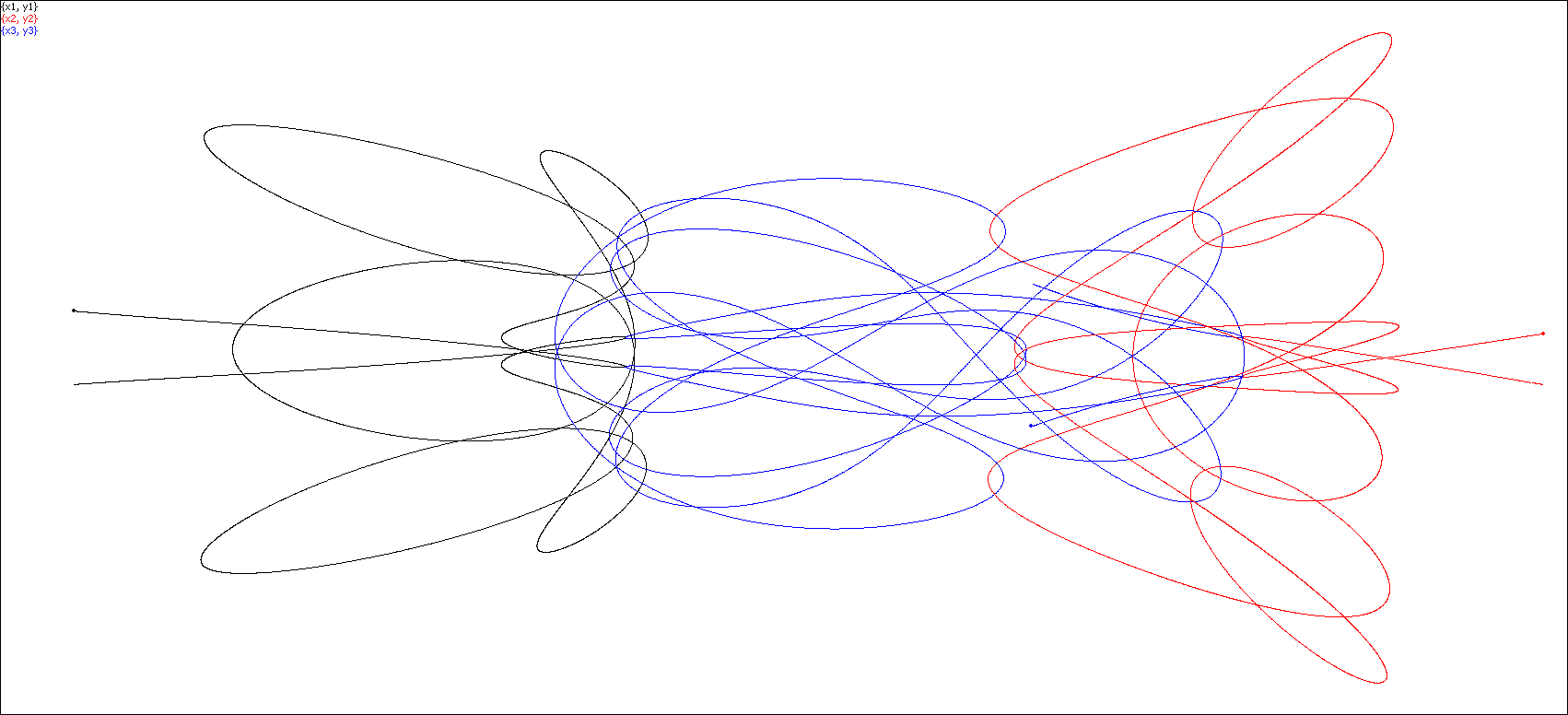
Simulation 24. No permutation.
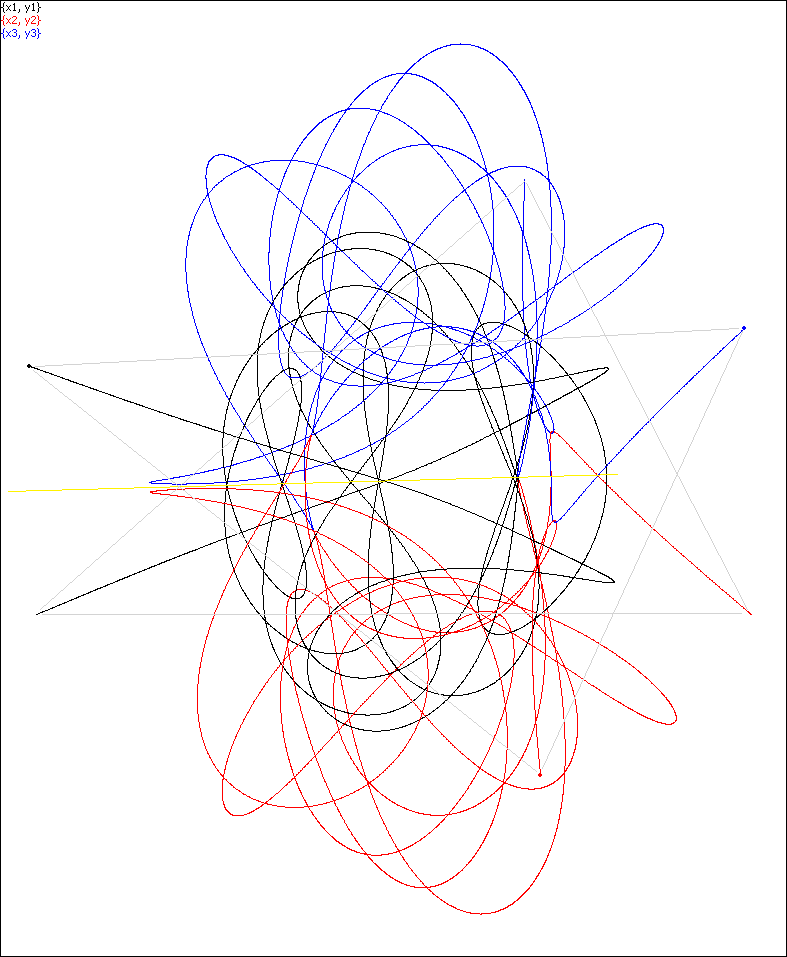
Simulation 26. Permutation (132)

Simulation 26. At the moment T/4 the bodies are in an isosceles
formation (rather than in syzygy).
The yellow line is the axis of symmetry.

Simulation 27. No permutation.